[论文分享] MiniONN: Oblivious Neural Network Predictions via MiniONN

September 22, 2023

User Privacy in Neural Networks

神经网络正变得无处不在，最近流行的 LLM 更是使神经网络从幕后走向了台前，让人们可以与之直接交互。到目前为止，GPT-4 仍然是效果最好的 LLM。当用户使用 GPT-4 服务时，会在 OpenAI 的网页输入提示词，这些用户输入的提示词会被发送到 OpenAI 的服务器，服务器经过 LLM 运算之后，再将结果返回给用户。然而，这样的交互方式有一个缺陷：用户输入对 OpenAI 而言是可见的。正因如此，一些大公司会禁止员工使用 GPT-4 处理敏感资料。

那么有没有什么办法可以使用大模型的同时，避免泄露用户数据呢？很显然，只需要把模型本地部署就好了。但是这样的方式并不现实，因为大模型 inference 对算力有一定的要求，并不是每个能打开浏览器的设备都可以运行；并且OpenAI 暂时还没有开源 GPT-4，市面上暂时也没有看到足够能打的开源竞品。

不能本地部署，那模型就得在云端服务器上，用户输入就一定得发送到服务端。这种情况下，还能做到保护用户隐私吗？这其实本质上是一个隐私计算问题。那我们对着常见的隐私计算方案数一数：联邦学习、多方安全计算（MPC）、可信执行环境（TEE）。联邦学习是做 training 用的，不是用于 inference 的，pass 掉。那剩下两种呢？熟悉 COMPASS 的同学可能以为我要开始介绍 TEE 了，毕竟这是我们实验室的传统艺能。的确，TEE 可以解决这里的问题，比如用 StrongBox 这样的 GPU TEE 来做 model inference，就可以做到用户输入对云服务商不可见。不过今天我们不讲 TEE，而是来探索一下 MPC 这条路能不能满足需求。

Oblivious Neural Network

今天要分享的文章名字很可爱：MiniONN（小黄人）。它发表在 CCS'17 上，作者是来自 Aalto University 的 Jian Liu 等人。作者提出了一个基于 2PC 和半同态加密的框架，可以将已经训练好的模型部署为 Oblivious Neural Network（ONN），即满足上述要求：model inference 过程中服务端无法得知 user input 的神经网络。

在 MiniONN 之前已经有不少 ONN 方面的工作，比如 CryptoNets、SecureML 等，但是这些方案有（1）需要重新训练、（2）不支持任意激活函数、（3）高开销和（4）准确率下降等问题。MiniONN 着手于解决这些问题。

MiniONN

一个神经网络一般来说有三种 layer：linear、activation、pooling，整个 model 就是三种 layer 的不断复合。值得注意的是，为了保证用户数据安全，层间的中间结果也是不能泄露的（参考 C. Orlandi 等人的文章），因此保密措施必须从头到尾全覆盖。

下面对每一种 layer 我们分别看看如何处理。首先 Linear layer 就是计算

y = Wx,

其中 $W$ 是权重矩阵， $x, y$ 分别是这一层的输入和输出。ONN 要求 server $\mathcal{S}$ 无法得知 $x$ 和 $y$ ，client $\mathcal{C}$ 无法得知 $W$ 。为此，MiniONN 引入了一个预处理阶段：在 model inference 正式开始之前， $\mathcal{S}$ 和 $\mathcal{C}$ 通过 2PC 协议共同商议一对 pair $(u,v)$ 使得 $u + v = W r$ ，其中 $r$ 是一个 $\mathcal{C}$ 生成的随机数，对 $\mathcal{S}$ 保密， $\mathcal{C}$ 拿到 $v$ ， $\mathcal{S}$ 拿到 $u$ 。正式计算阶段， $\mathcal{C}$ 把手里要保护的 $x$ 减掉刚刚的 $r$ ，发给 $\mathcal{S}$ 去计算， $\mathcal{S}$ 会算得 $W(x-r)$ 。 $\mathcal{S}$ 把结果加上 $u$ 之后发给 $\mathcal{C}$ ， $\mathcal{C}$ 拿到 $W(x-r)+u=Wx-v$ 。而 $v$ 是 $\mathcal{C}$ 已知的东西，加上去就可以拿到最终结果 $Wx$ 了。整个过程中最 nontrivial 的部分发生在预处理过程的 $(u,v)$ pair generation，这个步骤可以通过引入半同态加密来完成。

Activation function 相对来说更难处理一些。刚刚的预处理阶段利用到了 linearity，本质上是一种更强的同态（同时对向量加法和数乘相容），这使得 oblivious matrix multiplication 成为可能。但是 activation function 并没有这么好的性质，oblivious activation 会更困难一些。我们先考虑一种简单但是常见的 activation function， $ReLU$ ：

ReLU

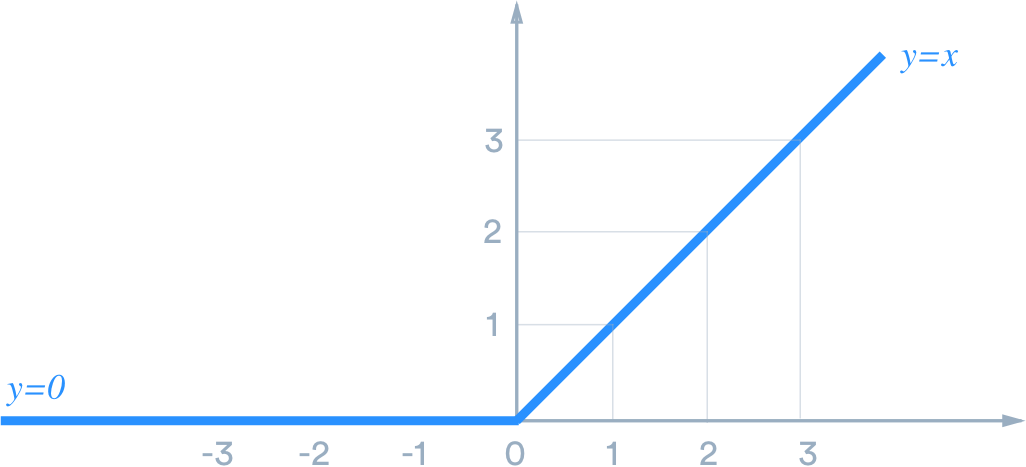
$ReLU$ 是一个分段函数，两段分别都是线性的，而线性的部分可以通过类似之前矩阵乘法的方式处理。那么如果我们能想办法进行 oblivious compare 的话，就相当于可以安全地 evaluate $ReLU$ 函数了。而 oblivious compare 也有现成的 2PC protocol 可以使用：使用 garbled circuit 来得到 $y$ （记得此前 $\mathcal{S}$ 手中只有不完整的 $y$ ，需要通过 garbled circuit 重建并确保 $y$ 不泄露），并计算 $b = compare(y,0)$ ， $b$ 的取值为 $0$ 或者 $1$ ，接下来只需要将 $b$ 乘以 $y$ 再返回即可。这个步骤最关键的部分在于 garbled circuit 这种 2PC 方案来完成 compare。

但是 $ReLU$ 毕竟是一个简单的函数，更复杂的 activation function 如何处理呢？MiniONN 采用的方案是：任意函数都可以用若干个线段拟合（描点连线），也就是说，我们把任意函数变成一个多段的分段函数，然后使用类似刚刚 $ReLU$ 的方案处理。文中 claim 这样的处理对准确率影响较低。

最后关于 pooling layer，一般是得到向量中的最大值或者平均值，这些都是 2PC 中很早就有成熟方案的问题了，不需要额外的构造。

综上，MiniONN 巧妙得 compose 了多种 2PC 技术，把整个 NN 变成了 ONN（因此文中证明过程采用的是 UC（Universal Composability）框架，让我花了很大功夫才逐渐理解）。

Experiments

MiniONN 在 MNIST、PTB 和 CIFAR-10 三个数据集上进行了测试。其中 MNIST 和 PTB 上性能表现还可以，但是 CIFAR-10 上性能很差，文中说原因是 CIFAR-10 相对比较大。

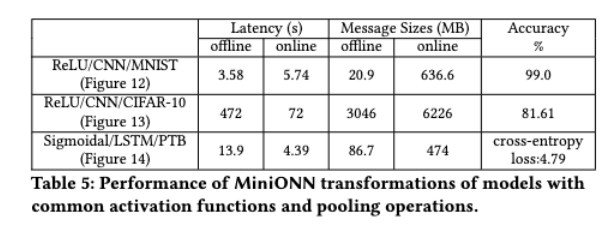
Experiment Results

Conclusion

MiniONN 用比较有创意的方案解决了 model inference 过程中的用户隐私问题。文中还提到了一些技术细节，比如如何处理浮点数、如何使用 SIMD 指令加速半同态计算等，在本文中没有仔细介绍，有兴趣的同学可以看原文。

不过 MiniONN 遗留了一些没有解决的问题：

缺少对 Softmax 激活函数的支持（文中认为可以不用支持 Softmax，但是在 2023 年的今天，这种 argument 已经站不住脚）；
没有提供 secure training 的支持；
设计中没有考虑使用 GPU 等加速器；
依赖网络连接，无法支持有低延迟需求的本地部署模型。

期待会有更巧妙的工作出现，解决这些问题。